Rosenbrock function
In mathematical optimization, the Rosenbrock function is a non-convex function used as a performance test problem for optimization algorithms introduced by Howard H. Rosenbrock in 1960[1]. It is also known as Rosenbrock's valley or Rosenbrock's banana function.
The global minimum is inside a long, narrow, parabolic shaped flat valley. To find the valley is trivial. To converge to the global minimum, however, is difficult.
It is defined by
It has a global minimum at  where
where 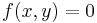 . A different coefficient of the second term is sometimes given, but this does not affect the position of the global minimum.
. A different coefficient of the second term is sometimes given, but this does not affect the position of the global minimum.
Contents |
Multidimensional generalisations
Two variants are commonly encountered. One is the sum of 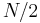 uncoupled 2D Rosenbrock problems,
uncoupled 2D Rosenbrock problems,
This variant is only defined for even  and has predictably simple solutions.
and has predictably simple solutions.
A more involved variant is
This variant has been shown to have exactly one minimum for 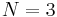 (at
(at 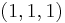 ) and exactly two minima for
) and exactly two minima for 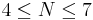 -- the global minimum of all ones and a local minimum near
-- the global minimum of all ones and a local minimum near 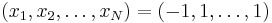 . This result is obtained by setting the gradient of the function equal to zero, noticing that the resulting equation is a rational function of
. This result is obtained by setting the gradient of the function equal to zero, noticing that the resulting equation is a rational function of  . For small
. For small  the polynomials can be determined exactly and Sturm's theorem can be used to determine the number of real roots, while the roots can be bounded in the region of
the polynomials can be determined exactly and Sturm's theorem can be used to determine the number of real roots, while the roots can be bounded in the region of 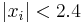 [4]. For larger
[4]. For larger  this method breaks down due to the size of the coefficients involved.
this method breaks down due to the size of the coefficients involved.
Stationary points
Many of the stationary points of the function exhibit a regular pattern when plotted[4]. This structure can be exploited to locate them.
Stochastic version
There are many ways to extend this function stochastically. In Xin-She Yang's functions, a generic or heuristic extension of Rosenbrock's function is given to extend this function into a stochastic function[5]
where the random variables  obey a uniform distribution Unif(0,1). In principle, this stochastic function has the same global optimimum at (1,1,...,1), however, the stochastic nature of this function makes it impossible to use any gradient-based optimization algorithms.
obey a uniform distribution Unif(0,1). In principle, this stochastic function has the same global optimimum at (1,1,...,1), however, the stochastic nature of this function makes it impossible to use any gradient-based optimization algorithms.
See also
Notes
- ^ Rosenbrock, H.H. (1960). "An automatic method for finding the greatest or least value of a function". The Computer Journal 3: 175–184. doi:10.1093/comjnl/3.3.175. ISSN 0010-4620.
- ^ L C W Dixon, D J Mills. Effect of Rounding errors on the Variable Metric Method. Journal of Optimization Theory and Applications 80, 1994. [1]
- ^ "Generalized Rosenbrock's function". http://www.it.lut.fi/ip/evo/functions/node5.html. Retrieved 2008-09-16.
- ^ a b Schalk Kok, Carl Sandrock. Locating and Characterizing the Stationary Points of the Extended Rosenbrock Function. Evolutionary Computation 17, 2009. [2]
- ^ Yang X.-S. and Deb S., Engineering optimization by cuckoo search, Int. J. Math. Modelling Num. Optimisation, Vol. 1, No. 4, 330-343 (2010)
References
- Rosenbrock, H. H. (1960), "An automatic method for finding the greatest or least value of a function", The Computer Journal 3: 175–184, doi:10.1093/comjnl/3.3.175, ISSN 0010-4620, MR0136042
External links
- Rosenbrock function plot in 3D
- Minimizing the Rosenbrock Function by Michael Croucher, The Wolfram Demonstrations Project.
- Weisstein, Eric W., "Rosenbrock Function" from MathWorld.
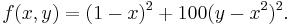
![f(\mathbf{x}) = f(x_1, x_2, \dots, x_N) = \sum_{i=1}^{N/2} \left[100(x_{2i-1}^2 - x_{2i})^2
%2B (x_{2i-1} - 1)^2 \right].](/2012-wikipedia_en_all_nopic_01_2012/I/2e4c03f8119f284d0453b31c7c9a573f.png)
![f(\mathbf{x}) = \sum_{i=1}^{N-1} \left[ (1-x_i)^2%2B 100 (x_{i%2B1} - x_i^2 )^2 \right] \quad \forall x\in\mathbb{R}^N.](/2012-wikipedia_en_all_nopic_01_2012/I/92ca2a9067744a5a80d44d66153690f1.png)
![f(\mathbf{x}) =\sum_{i=1}^{n-1} \Big[(1-x_i)^2%2B100 \epsilon_i (x_{i%2B1}-x_i^2)^2 \Big],](/2012-wikipedia_en_all_nopic_01_2012/I/d9d68bfbd78e5ef2e3f93051b8db3b87.png)